背景

christina04.hatenablog.com

で紹介したアーキテクチャの中にBloom Filterというものがありました。

今回はこちらの仕組みを説明します。

Bloom Filterとは

Bloom Filterは 偽陽性（無いのにあると回答）はあるが、偽陰性（あるのに無いと回答）はない ことでデータの存在有無をメモリ効率良く保持する確率的データ構造です。

具体的なユースケースとして

データベースのキャッシュ存在チェック
- データベースクエリやキャッシュへのアクセス前に、対象のデータが存在するかを事前にフィルタリング
分散システムでの存在チェック
- 分散システムや分散キャッシュにおいて、データが特定のノードに存在するかを事前に確認
- DynamoDB や Bigtable などでデータの分散配置を効率化し、データが「存在しない」と判断された場合にクエリを回避
推薦システム
- 動画配信サービスやECサイトの推薦アルゴリズムで、ユーザーにすでに推薦済みのアイテムを除外。

などがあります。

前回のLSM Treeは真ん中の分散システムでの存在チェックですね。

仕組み

なぜ前述のユースケースが実現できるかの仕組みをこれから説明します。

まず前提として

長さmのビット配列（初期はすべて0）
k個のハッシュ関数（例：h_0, h_1, h_2）

を用意します。

フロー

次にデータの追加や存在チェックのフローです。

1. 要素の追加（insert）

例として文字列 "apple" を追加します。

各ハッシュ関数で "apple" をハッシュしてビット配列のインデックスを得る
- たとえば [5, 17, 23]
ビット配列のそのインデックスを 1に設定

bit_array[5] = 1
bit_array[17] = 1
bit_array[23] = 1

2. 要素の存在確認（check）

文字列 "apple" が含まれているかをチェックします。

同じようにハッシュして [5, 17, 23] を得る
すべてのビットが1 → 「含まれている可能性がある」
どれか1つでも0 → 「絶対に含まれていない」

となります。

例えば文字列 "banana" の場合は、

同じようにハッシュして [3, 5, 11] を得る
[5]は"apple"のおかげでビット配列が1
しかし[3, 11]はビット配列が0 → 「絶対に含まれていない」

となります。

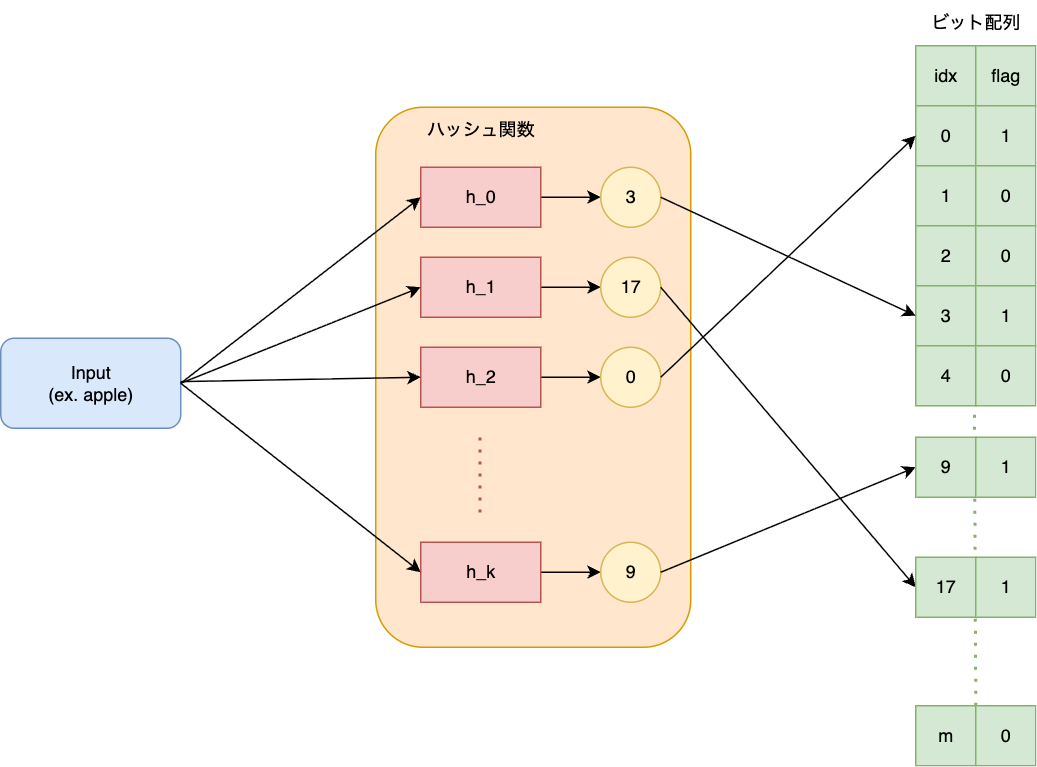
アーキテクチャ図

上記の説明を図で表すと以下の様になります。

メリット・デメリット

データ構造から分かるように、BloomFilterには次のメリット・デメリットがあります。

メリット

高速
メモリ使用率が非常に少ない
- 大規模データセットの存在確認やフィルタリング処理に向いている
偽陰性はない

デメリット

偽陽性がある
複数登録していくうちにビット列は上書きされて精度が悪くなる
- 衝突（collisions）と飽和（saturation）

偽陽性は次のようなケースです。

"apple" → ビット[5, 17, 23] = 1
"banana" → ビット[5, 41, 99] = 1

→ "grape" が [5, 17, 41] だと「含まれるかも」と誤判定される

この精度悪化に対して、

削除が可能なCounting Bloom Filter
要素数が増えて偽陽性率が増えてきたら、新しいBloom Filterを追加で作るScalable Bloom Filter

といった改善した仕組みがあったりします。

実装例

Go言語での実装例は以下です。

package main

import (
    "fmt"
    "hash/crc32"
    "hash/fnv"
)

type BloomFilter struct {
    bitset []bool
    size   uint32
}

// ハッシュ関数1（FNV）
func hash1(s string) uint32 {
    h := fnv.New32a()
    h.Write([]byte(s))
    return h.Sum32()
}

// ハッシュ関数2（CRC32）
func hash2(s string) uint32 {
    return crc32.ChecksumIEEE([]byte(s))
}

// Bloom Filter作成
func NewBloomFilter(size uint32) *BloomFilter {
    return &BloomFilter{
        bitset: make([]bool, size),
        size:   size,
    }
}

// 要素を追加
func (bf *BloomFilter) Add(s string) {
    h1 := hash1(s) % bf.size
    h2 := hash2(s) % bf.size

    for i := 0; i < 3; i++ { // k=3 の場合
        pos := (h1 + uint32(i)*h2) % bf.size
        bf.bitset[pos] = true
    }
}

// 存在チェック
func (bf *BloomFilter) Exists(s string) bool {
    h1 := hash1(s) % bf.size
    h2 := hash2(s) % bf.size

    for i := 0; i < 3; i++ { // k=3 の場合
        pos := (h1 + uint32(i)*h2) % bf.size
        if !bf.bitset[pos] {
            return false // 1つでも立ってなければ「存在しない」
        }
    }
    return true
}

// 実行例
func main() {
    bf := NewBloomFilter(1000)

    bf.Add("apple")
    bf.Add("banana")

    fmt.Println("apple:", bf.Exists("apple"))   // true
    fmt.Println("banana:", bf.Exists("banana")) // true
    fmt.Println("grape:", bf.Exists("grape"))   // false or true (偽陽性の可能性)
}

ポイントとして

複数のハッシュ関数を個別に用意するのは大変なので、ダブルハッシュという実質2つの関数で任意数のハッシュ関数をシミュレートできる形式を取っています。

func (bf *BloomFilter) Add(s string) {
    h1 := hash1(s) % bf.size
    h2 := hash2(s) % bf.size

    for i := 0; i < 3; i++ { // k=3 の場合
        pos := (h1 + i*h2) % bf.size
        bf.bitset[pos] = true
    }
}

まとめ

LSMツリーやキャッシュロジックの改善策であるBloom Filterについて、図と実装を用いて説明しました。

Carpe Diem

備忘録

Bloom Filter の仕組み

背景